Nel campo dell'Archeoastronomia la letteratura relativa all'esistenza vera o presunta, in taluni siti, di allineamenti diretti verso il punto di levata o di tramonto di oggetti astronomici è abbondante. Capita spesso di leggere che talune linee di pietre o buche di palo sarebbero orientate verso il punto di sorgere o di tramonto del Sole, della Luna o di qualche stella luminosa in corrispondenza di qualche data o posizione particolare. 

Il Sole e la Luna sono astri molto luminosi che possono essere osservati non appena il loro lembo superiore fa capolino al limite dell'orizzonte locale apparente o di quello fisico se nel luogo considerato esistono dei rilievi che si elevano di alcuni gradi sopra l'orizzonte astronomico. Talvolta si legge anche di orientazioni stellari e generalmente nella letteratura viene preso in considerazione, dopo le debite correzioni per la rifrazione atmosferica, l'azimut di levata della stella all'orizzonte astronomico locale.

In realtà un simile approccio non è metodologicamente corretto in quanto non vengono quasi mai presi in considerazione gli effetti dell'estinzione atmosferica la quale gioca un ruolo determinante facendo si che la stella diventi visibile solamente quando la sua altezza rispetto all'orizzonte astronomico locale abbia già raggiunto un consistente valore, che chiameremo in questa sede "altezza di prima visibilità", abbreviata in HPV. La HPV dipende grosso modo dalla trasparenza dell'atmosfera in prossimità dell'orizzonte in direzione della stella che sorge e dalla sua magnitudine visuale apparente. In letteratura possiamo trovare il termine "angolo di estinzione" per designare HPV e qualche studio relativamente ad esso è stato fatto in passato.

L'archeoastronomo A. Thom (1967) propose una semplice regola messa a punto da O. Neugebauer sulla base di antiche osservazioni stellari registrate su tavolette babilonesi. La regola di Thom-Neugebauer ci dice che una stella di magnitudine visuale "m" diverrà visibile nel cielo mattutino ad un'altezza sull'orizzonte approssimativamente pari alla sua magnitudine visuale. In questo modo una stella di prima magnitudine diverrà visibile a 1 grado di altezza sull'orizzonte astronomico locale. Una di seconda magnitudine sarà visibile a due gradi e cosi via. Al tramonto le cose si invertono nel senso che la stella di seconda magnitudine sparirà al tramonto a due gradi dall'orizzonte, quella di prima grandezza ad un grado e così via. 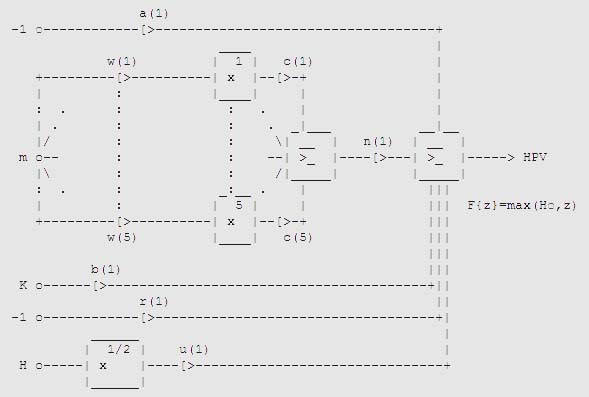La dipendenza di HPV dalla trasparenza atmosferica può essere tecnicamente quantificata mediante il coefficiente di estinzione atmosferica K nella
banda visuale ben noto a chi lavora nel campo della fotometria fotoelettrica.

I fotometristi sanno determinare sperimentalmente notte per notte il valore di K, per le lunghezze d'onda di osservazione, ma volendo stimare l'azimut di prima visibilità di una stella ad esempio 3000 anni fa, nessuna determinazione sperimentale è ovviamente possibile. Gli effetti dell'estinzione atmosferica agiscono grosso modo sul cammino dei fotoni provenienti dalla stella attraverso tre differenti strati all'interno dell'atmosfera terrestre.

Il primo strato importante è quello della fascia di ozono a circa 20 Km di altezza dal suolo, il secondo è quello che si stende a circa 8.2 Km di quota e contribuisce al cosiddetto "Rayleigh scattering" e il terzo è lo strato degli aerosols, posizionato a circa 1500 metri di altezza e in cui possiamo trovare particelle di acqua nebulizzata, polveri portate dal vento, pollini degli alberi e altre particelle solide che interagiscono con la luce che giunge dalla stella.

In letteratura è possibile reperire alcuni modelli utili alla quantificazione degli effetti di estinzione attraverso i vari strati. Ad esempio Hayes e Latham (1975) si sono occupati di tutte e tre le zone, Bower e Ward (1982) si sono occupati dello strato di ozono e vari autori, tra i quali Shafer (1993) si sono occupati dello strato in cui predominano gli aerosols. Una formula rigorosa e chiusa per mettere in relazione "m" e "Kv" non esiste, ma esistono dati sperimentali e dati di simulazione al computer ottenuti da Schafer e Liller (1990) a cui è possibile fare riferimento. 

Al fine di stabilire un algoritmo di calcolo pratico sufficientemente semplice risulta molto utile applicare una rete neuronale artificiale e addestrarla sui dati sperimentali disponibili sia derivanti dalle simulazioni che dalle osservazioni chiedendo ad essa di ottimizzare una forma funzionale approssimata, ma sufficientemente accurata.  Esaminando i modelli messi a punto da questi autori siamo in grado di estrarre le informazioni che ci permettono di mettere a punto la topologia iniziale (mesostruttura) della rete neuronale artificiale da addestrare in modo che l'approssimazione ottenuta permetta di predire con un buon margine di affidabilità l'altezza di prima visibilità delle stelle in funzione della loro magnitudine e di alcuni parametri atmosferici locali e dell'incertezza con cui la valutazione di HPV è possibile. Nota HPV la sua conversione nell'"azimut di prima visibilità" ad una data latitudine geografica diventa solamente una questione di semplice calcolo trigonometrico.

Impiegando le funzioni che descrivono la "massa d'aria" pertinenti a ciascun strato, è stato possibile mettere a punto un modello numerico capace di fornire la HPV di una stella in funzione della sua magnitudine visuale apparente, della latitudine geografica e della quota sul livello del mare del luogo e del tasso di umidità relativa dell'aria. Il problema è comunque mal determinato e il grado di incertezza insito in esso è molto elevato, tale da richiedere l'utilizzo di particolari tecniche matematiche di valutazione quali sono le reti neuronali artificiali dette a Link Funzionale, sviluppate per la prima volta da Pao (1989) al fine di migliorare la potenza di calcolo delle reti neuronali artificiali, aumentandone la capacità di approssimare il comportamento di sistemi nonlineari, diminuendo nel contempo il tempo richiesto dalla fase di apprendimento. Tornando al presente problema, la mesostruttura ritenuta più efficiente per permettere alla rete neuronale artificiale di stimare HPV è stata la seguente:

Formata da una sottorete FLN a cinque link funzionali nonlineari più un elemento sommatore e da un neurone addizionale con attivazione a rampa capace di aggiungere gli effetti dovuti alla rifrazione atmosferica e alla quota del sito. La fase di apprendimento ha permesso di arrivare alla determinazioni del seguente insieme ottimale di pesi:

ottenuti minimizzando l'energia complessiva della rete. Il modello proposto è quindi il seguente:

                                                 _5_             j                   1/2
HPV = max{Ho, a(1)+ b(1) K + n(1) >__ c(j) w(j) m - r(1) + u(1) H }
                                                  j=1

in cui il peso sinaptico r(1) è il contributo R della rifrazione atmosferica, calcolato analiticamente più avanti, H è la quota del sito rispetto al livello del mare (in Km), K è il coefficiente di estinzione atmosferica che misura il cammino ottico totale verso lo zenith e che è misurato in magnitudini per unità di massa d'aria, Ho è l'altezza apparente dell'orizzonte fisico rispetto a quello astronomico. Il contributo dovuto alla rifrazione astronomica può essere valutato  mediante la seguente relazione:

      0.00467 P exp(-H/8.4)
R = -----------------------------------
     (273 + T) tan[Hm + 7.31/(Hm + 4.4)]

in funzione della pressione atmosferica P (in millibar), della temperatura dell'aria T in oC, della quota dell'osservatore H (in Km) e dell'elevazione Hm che vale:

                                                                  (0.6 K + 0.29) m          1/2
Hm = max{ Ho, -2.71 + 11.7 K + ( 2 K + 0.7) e                          -(H/Hp) }

che rappresenta l'altezza di prima visibilità, ottenuta trascurando la rifrazione atmosferica, in cui Hp=1.1 Km. Il coefficiente di estinzione è legato alla profondità ottica "q" nel modo seguente:

K = 1.086 q

K = -2.5 Log(T) 

                           2   -H/Hr     4
 Kr = 113700 (n-1)    e        Wl 

Ko = 0.031 + 0.0041 [ f cos(As) - cos(3 f) ]